Binary logistic regression is a method used to solve binary classification problems. In binary logistic regression, our goal is to divide the sample into two categories based on the given features, usually represented by 0 and 1. Logistic regression utilizes a mapping function called a logistic function (or sigmoid function) to map linearly combined features to a probability value between 0 and 1. By setting a threshold, we can determine the classification of samples based on the predicted probability values.

    Data description:

    Background description:

    Binary logistic regression is a statistical model used to handle binary classification problems. It is based on a linear combination of input features and uses an objective function (also known as a sigmoid function) to probabilistic the results, thereby predicting the probability that the sample belongs to a certain category. In this analysis, researchers want to understand whether being an only child (yes or no) is influenced by several independent variables (A1, A2). Researchers used binary logistic regression models to construct predictive models.

    The analysis results are as follows:

    Using ['A1 ',' A2 '] as independent variables and whether it is an only child as the dependent variable for binary logistic regression analysis, it can be seen from the above table that a total of 80 samples participated in the analysis.

     Based on the analysis of the overall effectiveness of the model, it can be seen from the table that the original hypothesis for model testing here is: whether to include independent variables ['A1 ',' A2 '] when the model quality is the same in both cases; The p-value here is greater than 0.05, indicating acceptance of the original assumption. This means that the independent variables added during the model construction are meaningless, indicating that the model construction is meaningless, and subsequent indicator results are meaningless.

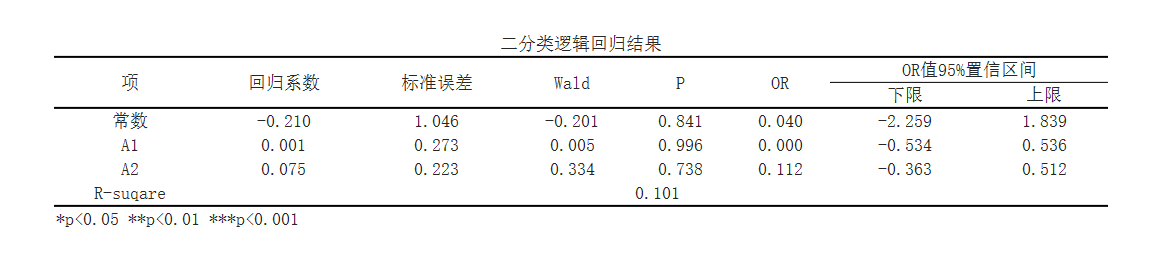
     From the above table, it can be seen that using ['A1 ',' A2 '] as the independent variable and whether one is an only child as the dependent variable for binary logistic regression analysis, it can be seen from the above table that the independent variable can explain the 0.101% change in the dependent variable. The results showed that none of the independent variables had a significant impact on whether the dependent variable was an only child (p>0.05).

    From the table above, it can be seen that the model formula is: ln (p/1-p)=-0.2101+0.0013 * A1+0.0746 * A2 (where p represents the probability of being an only child as 1 and 1-p represents the probability of being an only child as 0).

     The p-value here is greater than 0.05 (Chi=2.49, p=0.778>0.05), indicating acceptance of the original hypothesis, indicating that the model passed the HL test and had a good fit.

    Reference:

    [1]姜广辉，张凤荣，陈军伟等.基于Logistic回归模型的北京山区农村居民点变化的驱动力分析． 《 CNKI;WanFang 》，2007

    [2]谢花林，李波.基于logistic回归模型的农牧交错区土地利用变化驱动力分析——以内蒙古翁牛特旗为例． 《 CNKI;WanFang 》，2008

    [3]朱丽，王声湧，范存欣等.高校青年教师亚健康危险因素Logistic回归分析．《 中国公共卫生 》，2003

    [4]王阶，李军，姚魁武，衷敬柏.冠心病心绞痛证候要素和冠脉病变的Logistic回归分析．CNKI;WanFang 》，2007

    [5]庞素琳.Logistic回归模型在信用风险分析中的应用．《 数学的实践与认识 》，2006

关注微信公众号发送【示例数据】获取SPSSMAX练习示例数据。