Robust regression is a statistical method used to handle the impact of outliers or data deviations and improve the robustness of regression models. In traditional linear regression, outliers or data deviations often have a significant impact on the fitting of the model, resulting in inaccurate estimation of regression coefficients.

    Robust regression can effectively deal with these outliers or data deviations by using robust estimation methods, thus obtaining more reliable and robust regression results. In practical applications, Robust regression is a method that can handle the impact of outliers or data deviations. By using robust estimation and weight allocation, more robust and reliable regression coefficient estimates can be obtained.

    For data with outliers or data deviations, Robust regression can provide more accurate regression results and enhance the stability and reliability of the model.

    Data description:

    Background description:

    Robust regression analysis is usually used in the presence of outliers or outliers, which can improve the robustness of regression models and reduce the impact of outliers on the results. In this analysis, we used Robust regression analysis to investigate the impact of different indicator variables on the dependent variable in 81 samples. By explaining the regression coefficients and significance of each indicator variable, we can understand the degree to which each indicator affects the dependent variable.

    In this analysis, we focus on the impact of various indicator variables (A1, A2, A3, A4) on the dependent variable (A5). The regression coefficient represents the average impact of the indicator variable on the dependent variable, and the standard error measures the uncertainty of this estimation. The t-value and corresponding p-value are used to test whether the regression coefficient is significant. Through the 95% confidence interval, we can determine the range of regression coefficients.

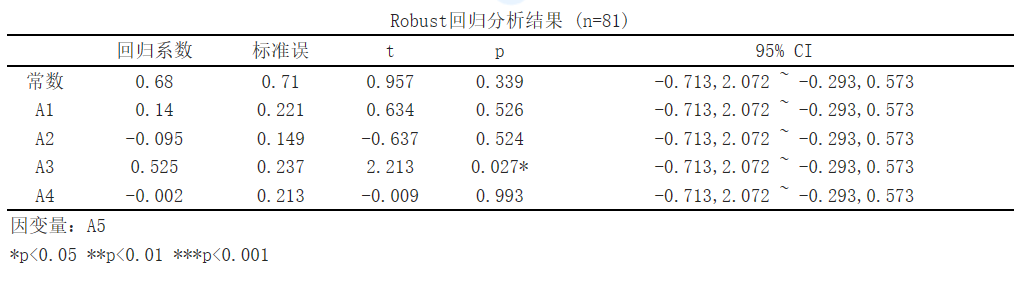
     The results of Robust regression analysis showed that A1 had no significant impact on A5, A2 had no significant impact on A5, A3 had a positive impact on A5, and A4 had no significant impact on A5.

关注微信公众号发送【示例数据】获取SPSSMAX练习示例数据。