Two way ANOVA has two types: one is a non interactive two way ANOVA, which assumes that the effects of factor A and factor B are independent of each other and there is no correlation; The other is a two-way ANOVA with interaction, which assumes that the combination of factor A and factor B will produce a new effect.

    Data description:

     Two factor analysis of variance is a statistical method used to study the impact of two or more independent variables on the dependent variable. In this context, we conducted an experiment to investigate the impact of two independent variables (factors) A1 and A2 on a certain SAS. We set 4 levels for each factor and observed the impact of these levels on the indicators.

    The analysis results are as follows:

    The results showed that there were two independent variables with significant differences in the dependent variable.

    A bivariate analysis of variance was conducted on the impact of A1 and A2 on the total score of SAS. The results showed that the p-value of item A1 was 0.0<0.05, indicating a significant difference in the dependent variable among different A1 items (F=16.428, p=0.0).

    A bivariate analysis of variance was conducted on the impact of A1 and A2 on the total score of SAS. The results showed that the p-value of item A2 was 0.001<0.05, indicating significant differences in the dependent variable among different A2 items (F=6.274, p=0.001).

    SPSSMAX also outputs line charts from different angles.

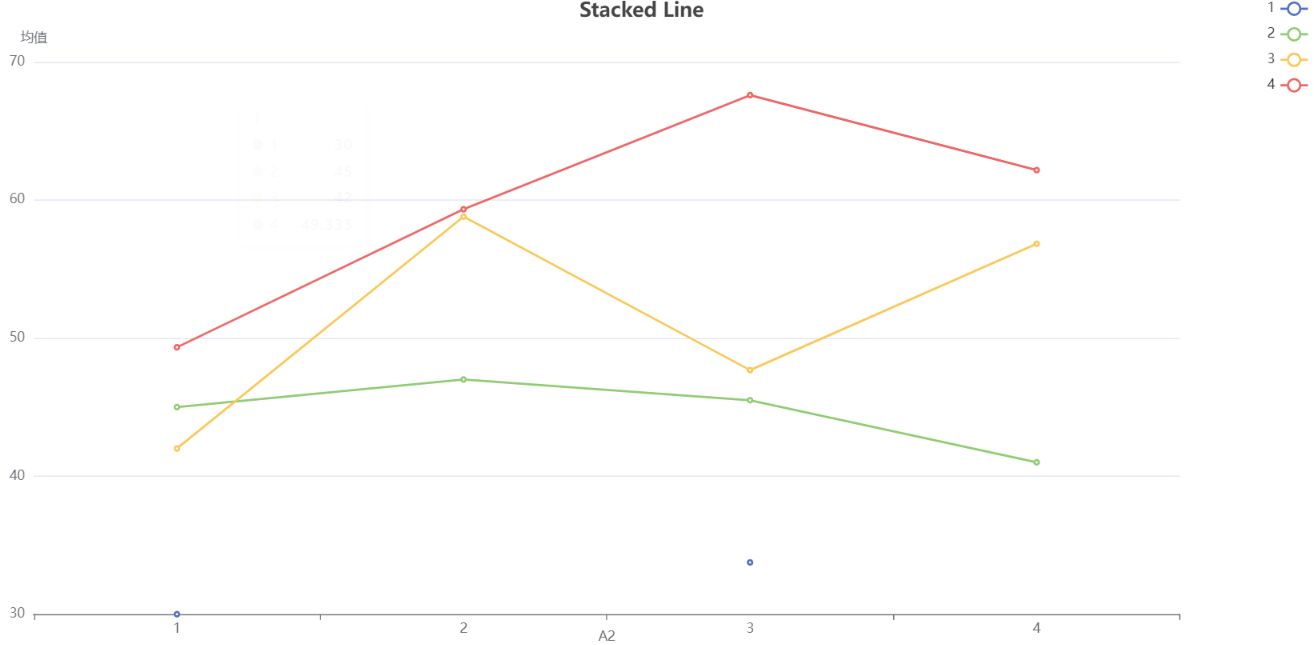
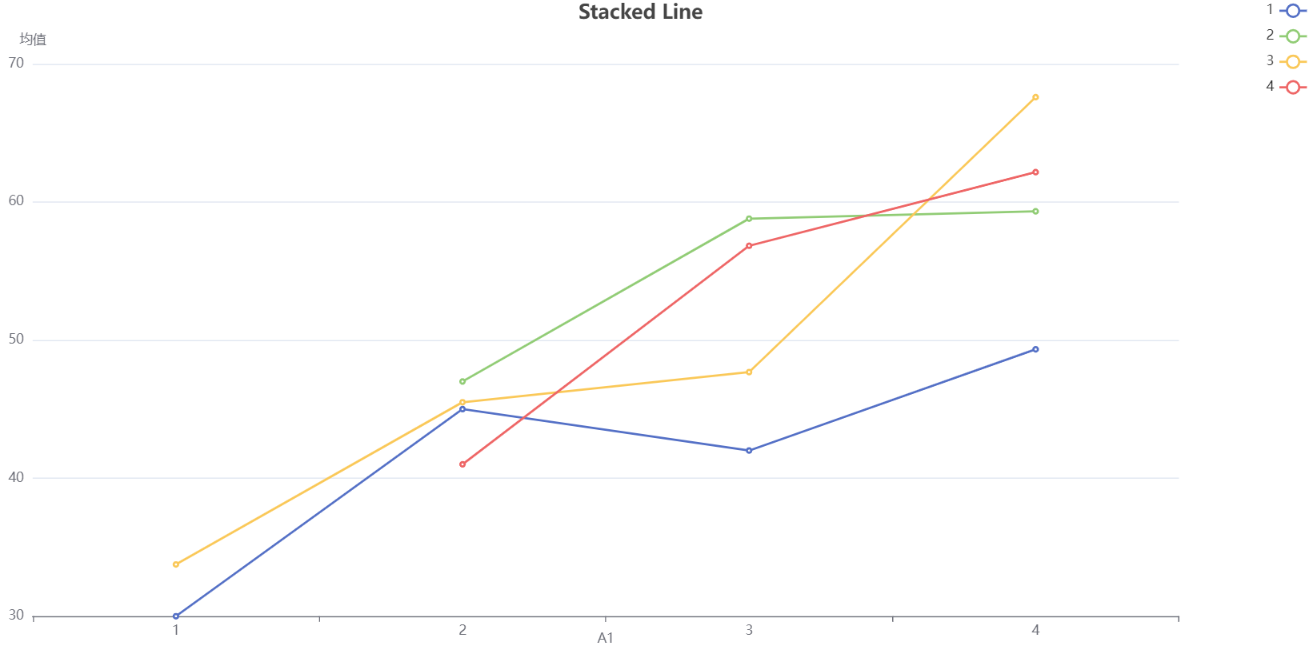
The simple effect graph after conducting a bivariate analysis of variance is used to explain and display the differences and interactions between different levels of factors.

Simple effect graphs can help us understand and reveal whether there is an interaction between two independent variables (factors) and the dependent variable, as well as the form of the interaction. It plots the mean or effect values of the dependent variable under different combinations of independent variable levels on a graph, allowing us to intuitively compare the differences between different combinations.

The functions of simple effect graphs include:

1. Revealing the main effect: Through a simple effect graph, we can see the mean difference of each independent variable at the level of other independent variables, thus determining whether there is a main effect. If there is a significant difference between the mean values under different combinations of independent variable levels, it can be considered that there is a main effect.
2. Analyzing interaction: Simple effect graphs can help us determine whether there is interaction between two independent variables. If there is a crossover or intersection between the mean values under different combinations of independent variable levels, it can be considered that there is an interaction.
3. Explain the form of interaction: Simple effect graphs can help us understand and explain the form of interaction. By observing the mean differences under different combinations, we can infer whether the interaction is enhanced or weakened, and its specific form.

In summary, simple effect graphs are an important tool for conducting bivariate analysis of variance, which can help us intuitively understand and explain the impact and interaction of two independent variables on the dependent variable.

Conclusion:

Explanation of bivariate analysis of variance results: In the results of bivariate analysis of variance, the total SAS scores we focus on are A1, A2, and A1: A2 (interaction), respectively. Here, "degree of freedom" represents the number of levels of each factor or interaction minus 1. The sum of squares represents the sum of the squares of each term. The 'mean square' represents the ratio of the sum of squares of each term to the degree of freedom. The 'F' value is the mean square ratio. 'p' is the significance level of each item obtained through statistical calculation

For factor A1, we found that A1 has a significant impact on the total SAS score (p < 0.05). Specifically, there is a significant average difference between the three levels of A1. In post hoc multiple comparisons, we compared the average differences between different levels in A1. The results showed that there were significant differences in the average values between A1 levels 1 and 3, as well as between A1 levels 1 and A1 levels 4 (p < 0.05). This means that under the A1 factor, there is a significant difference between different levels, that is, the A1 level has an impact on the total SAS score

For factor A2, we found that A2 had no significant effect on the total SAS score (p>0.05). Specifically, the average difference between the three levels of A2 is not significant. This means that under the A2 factor, the differences between different levels have no significant impact on the total SAS score

The results of interaction A1: A2 showed that the interaction between A1 and A2 had no significant impact on the total SAS score (p>0.05). This means that the combined effect of A1 and A2 did not have a significant impact on the total SAS score

In summary, based on the results of the bivariate analysis of variance, we can conclude that A1 factor has a significant impact on the total SAS score, while A2 factor and the interaction between A1 and A2 have no significant impact on the total SAS score

关注微信公众号发送【示例数据】获取SPSSMAX练习示例数据。