单位根检验(ADF)

单位根检验(ADF)是一种常用的时间序列分析方法，用于确定一个时间序列是否具有单位根（即非平稳性）。单位根是指随时间变化的趋势在长期上是持续的，而不会收敛到一个稳定的均值。ADF检验是基于自回归模型的检验方法，其中包含一个滞后项。它的原假设是存在单位根，即时间序列是非平稳的。

如果ADF检验的计算结果拒绝了原假设，即在给定的显著性水平下，可以认为时间序列是平稳的。在实际应用中，ADF检验是一种常用的时间序列分析方法，用于确定时间序列是否具有单位根。它的计算过程基于自回归模型，并通过对时间序列进行差分操作来消除趋势的影响。通过与临界值的比较，可以判断时间序列是否是平稳的。

数据说明：

ADF（Augmented Dickey-Fuller）检验是一种常用的单位根检验方法，用于检验时间序列数据中是否存在单位根（非平稳性）。在金融、经济学和其他领域的时间序列分析中，ADF检验被广泛用于确定一个变量是否具有平稳性。

分析结果如下所示：

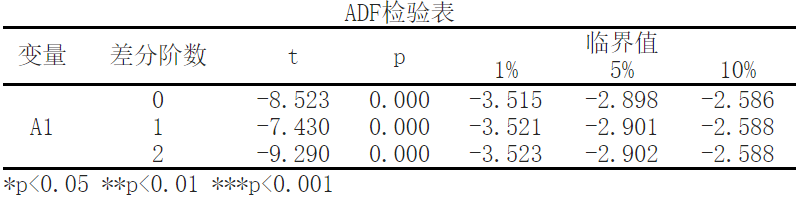
该序列检验的结果显示，在差分为0阶时，显著性P值< 0.05，水平上呈现显著性，因此拒绝原假设，说明该序列为平稳的时间序列。

该序列检验的结果显示，在差分为1阶时，显著性P值> 0.05，水平上没有呈现显著性，因此接受原假设，说明该序列不为平稳的时间序列。

该序列检验的结果显示，在差分为2阶时，显著性P值> 0.05，水平上没有呈现显著性，因此接受原假设，说明该序列不为平稳的时间序列。

背景说明：

ADF检验结果表解释：

在您提供的检验结果表中，包含了变量、差分阶数、t值、p值以及临界值。让我们逐个解释每个指标。

变量：您提供的ADF检验结果表中，第一列是变量的名称。在这个例子中，变量被标记为"A1"和"A2"。
差分阶数：第二列表示进行了多少次差分。差分是对时间序列数据进行一阶或多阶的差分运算，以消除非平稳性。在这个例子中，"A1"变量没有进行差分（差分阶数为0）。
t值：第三列是ADF检验的统计量，即t值。它用于衡量变量的平稳性。一般来说，如果t值小于临界值，就可以拒绝原假设，即存在单位根，表示非平稳性；如果t值大于临界值，就接受原假设，即不存在单位根，表示平稳性。在这个例子中，"A1"变量的t值为-8.523，"A2"变量的t值未提供。
p值：第四列是p值，也被用于检验变量的平稳性。p值表示给定样本观测到的统计量大小的概率。通常，如果p值小于显著性水平（如0.05），可以拒绝原假设，表明存在单位根，表示非平稳性；如果p值大于显著性水平，就接受原假设，表明不存在单位根，表示平稳性。在这个例子中，"A1"变量的p值为0.000，"A2"变量的p值未提供。
临界值：最后三列是临界值，以供对比。这些临界值是根据检验的置信水平来确定的，常见的置信水平有1%、5%和10%。如果t值小于临界值，可以拒绝原假设，表示数据非平稳。在这个例子中，对于"A1"变量，1%置信水平的临界值为-3.515，5%置信水平的临界值为-2.898，10%置信水平的临界值为-2.586。

综上所述，通过ADF检验结果表中的t值、p值及与临界值的比较，可以判断变量是否具有平稳性。如果p值小于显著性水平，且t值大于临界值，那么我们可以认为该变量是平稳的。否则，如果p值较大，或者t值小于临界值，那么我们将接受非平稳性的假设。

ADF检验图是一种用于可视化ADF检验结果的图表。它通常是一个折线图，横轴表示差分阶数，纵轴表示ADF统计量的值。在图表中，我们可以观察到ADF统计量在不同差分阶数下的变化情况。

ADF检验图的作用是帮助我们判断时间序列数据的平稳性。通过观察ADF统计量在不同差分阶数下的趋势，我们可以确定最佳的差分阶数，以消除非平稳性。如果ADF统计量在差分阶数增加后逐渐趋于稳定，即呈现一个水平的趋势，那么我们可以认为时间序列数据是平稳的。

ADF检验图还可以用于比较不同变量的平稳性。通过将多个变量的ADF检验结果绘制在同一张图上，我们可以直观地比较它们的平稳性。如果某个变量的ADF统计量的值更接近于零，且在差分阶数增加后趋于稳定，那么我们可以认为该变量更具有平稳性。

综上所述，ADF检验图是一种有助于判断时间序列数据平稳性的可视化工具，可以帮助我们选择合适的差分阶数以及比较不同变量的平稳性。

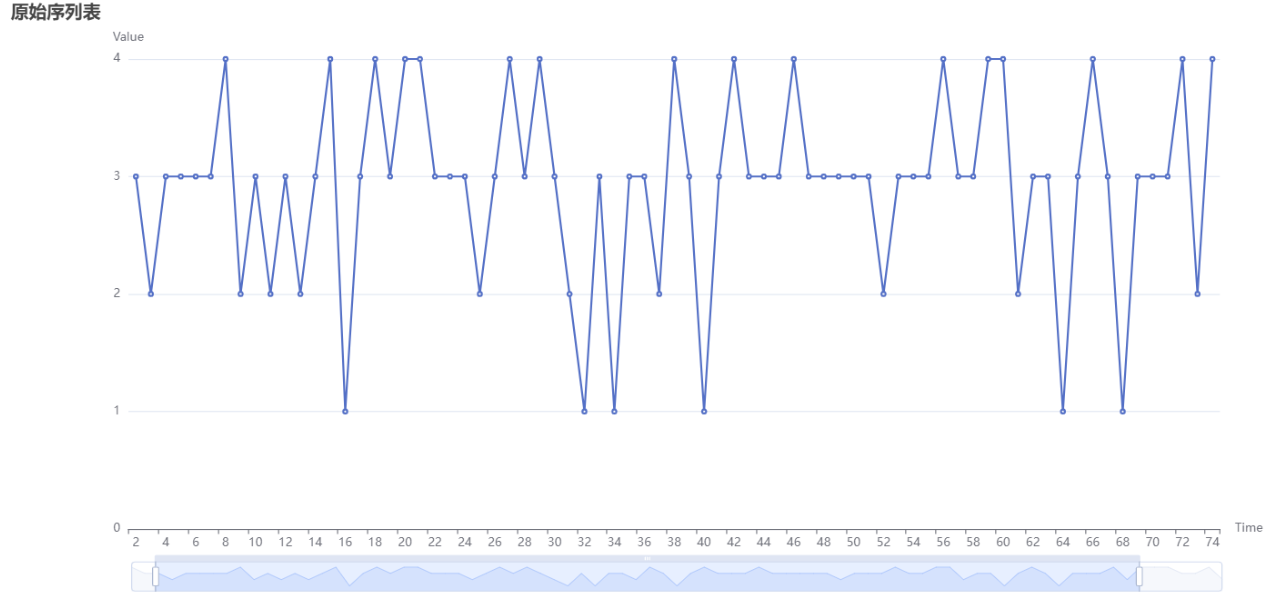
上图展示了未进行差分的原始图。其中X轴代表时间项，Y轴代表数值。

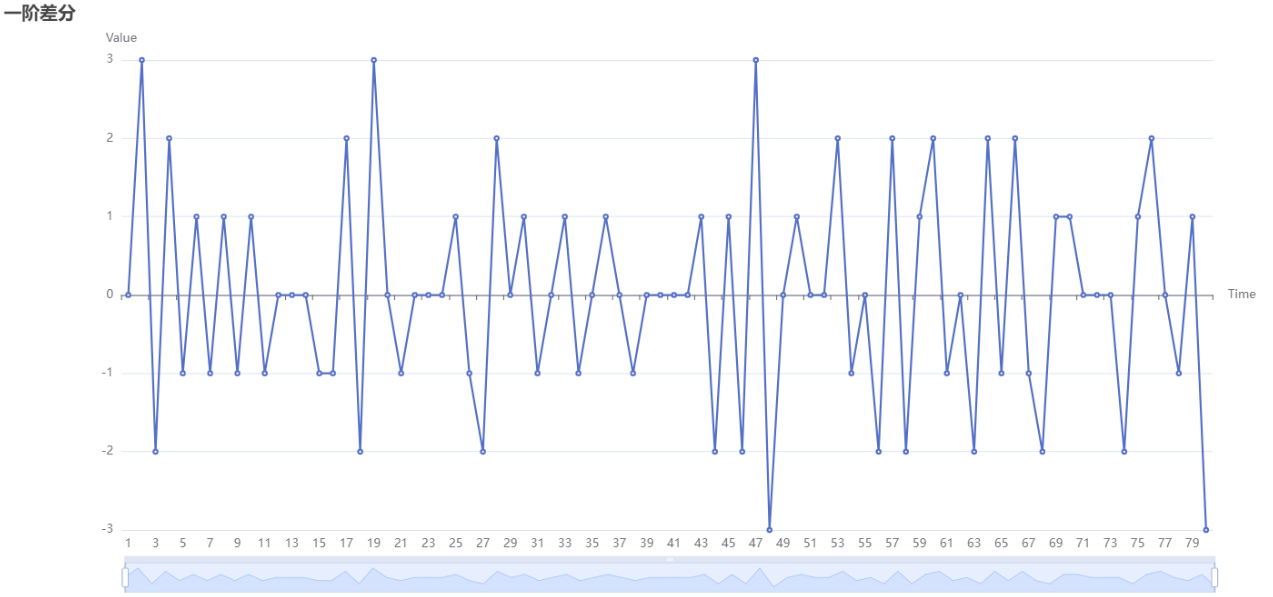
上图展示了进行一阶差分的结果图。当时间间距相等时，用下一个数值，减去上一个数值，得到一阶差分。

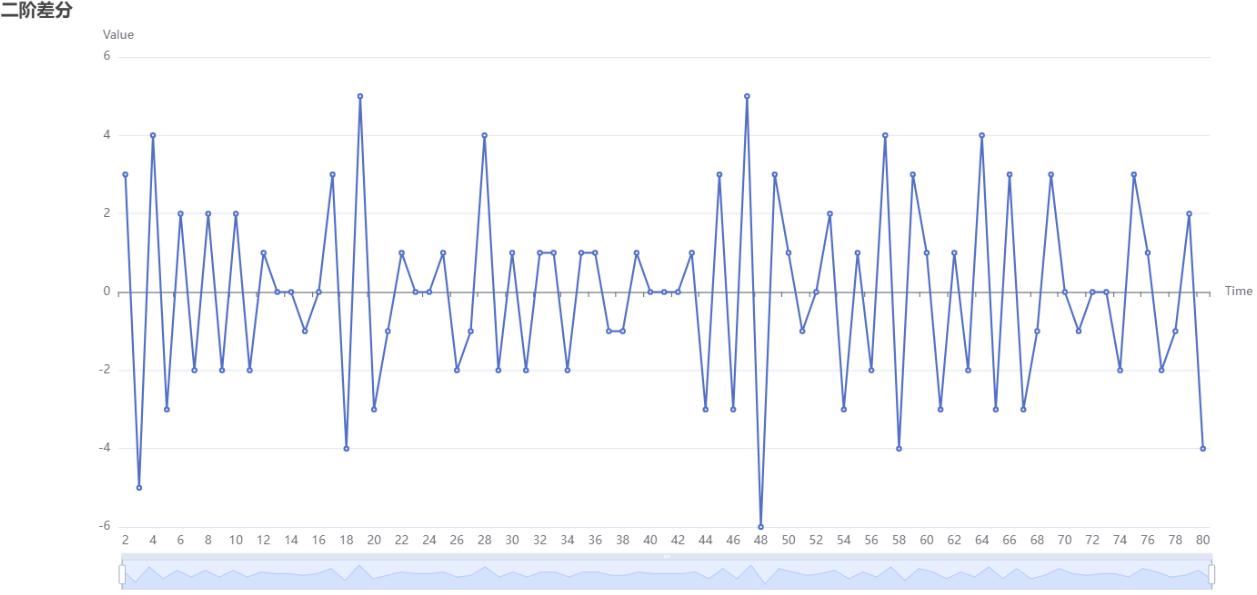
上图展示了进行二阶差分的结果图。做两次相同的动作，即再在一阶差分的基础上用后一个数值再减上一个数值一次，就叫“二阶差分”。

单位根检验(ADF)

关注微信公众号发送【示例数据】获取SPSSMAX练习示例数据。