双因素方差分析
双因素方差分析(Two-way ANOVA)有两种类型:一个是无交互作用的双因素方差分析,它假定因素A和因素B的效应之间是相互独立的,不存在相互关系;另一个是有交互作用的双因素方差分析,它假定因素A和因素B的结合会产生出一种新的效应。
数据说明:

双因素方差分析是一种统计方法,用于研究两个或更多个自变量对因变量的影响。在这个背景下,我们进行了一项实验来研究两个自变量(因素)A1和A2对某个SAS的影响。我们对每个因素设置了4个水平,并观察了这些水平对指标的影响。
分析结果如下所示:

结果显示,有2个自变量在因变量上存在显著差异。

对A1和A2对SAS总分的影响进行双因素方差分析,结果显示,其中项 A1的 p值为 0.0<0.05,说明不同A1项在因变量上存在显著差异(F=16.428,p=0.0)。
对A1和A2对SAS总分的影响进行双因素方差分析,结果显示,其中项 A2的 p值为 0.001<0.05,说明不同A2项在因变量上存在显著差异(F=6.274,p=0.001)。

SPSSMAX还输出不同角度的折线图。
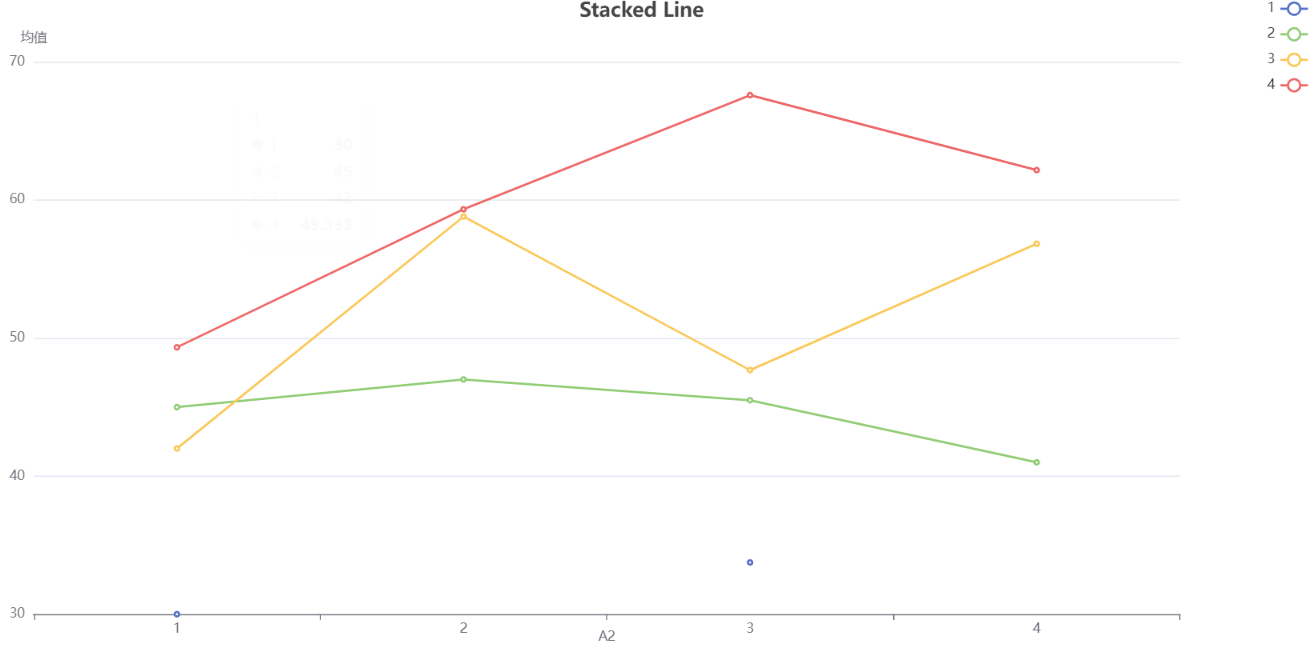
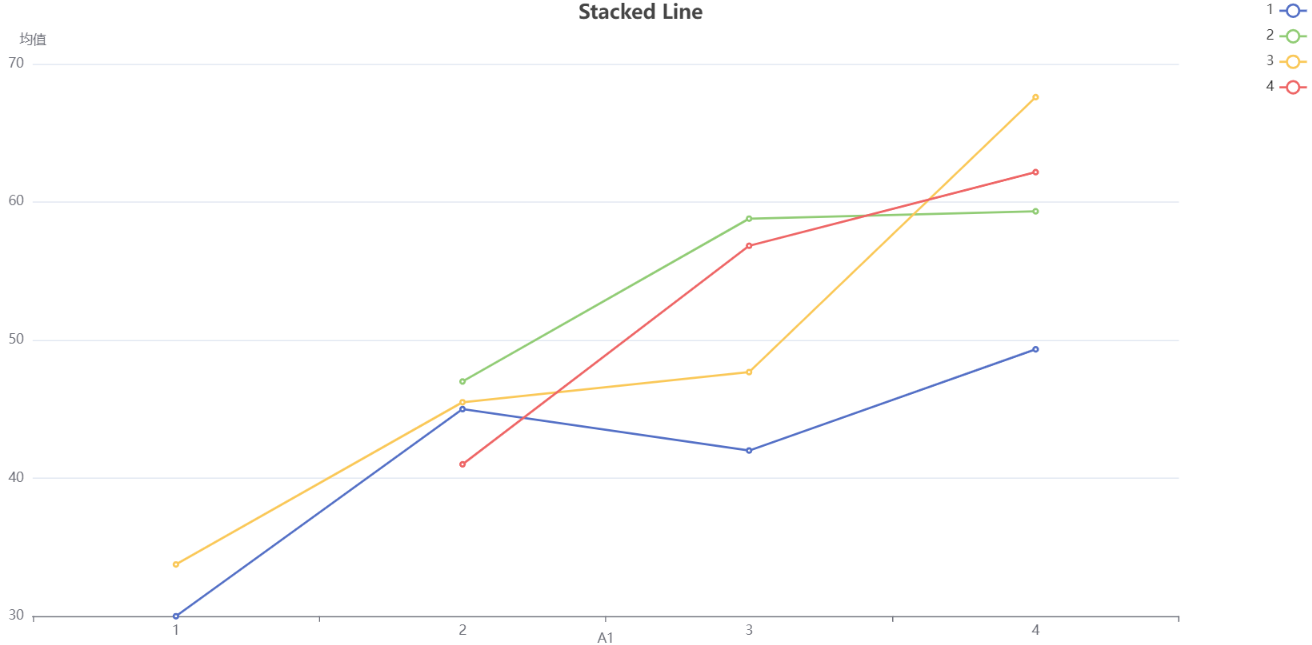
进行双因素方差分析之后的简单效应图形是用于解释和展示不同因素水平之间的差异和交互作用的。
简单效应图形可以帮助我们理解和揭示两个自变量(因素)对因变量的影响是否存在交互作用,以及交互作用的形式。它将因变量在不同自变量水平组合下的均值或效应值绘制在图形上,使我们能够直观地比较不同组合之间的差异。
简单效应图形的作用包括:
- 揭示主效应:通过简单效应图形,我们可以看到每个自变量在其他自变量水平上的均值差异,从而判断是否存在主效应。如果不同自变量水平组合下的均值之间存在明显差异,那么可以认为存在主效应。
- 分析交互作用:简单效应图形可以帮助我们判断两个自变量是否存在交互作用。如果不同自变量水平组合下的均值之间存在交叉或交叉点,那么可以认为存在交互作用。
- 解释交互作用的形式:简单效应图形可以帮助我们理解和解释交互作用的形式。通过观察不同组合下的均值差异,我们可以推断交互作用是增强型还是减弱型,以及其具体形式。
总之,简单效应图形是进行双因素方差分析后的重要工具,它能够帮助我们直观地理解和解释两个自变量对因变量的影响和交互作用。
结论:
双因素方差分析结果解释:在双因素方差分析的结果中,我们关注的SAS总分分别是A1、A2和A1:A2(交互作用)。这里,"自由度"表示每个因素或交互作用的级别数减1。"平方和"表示每个项平方和的总和。"均方"表示每个项平方和与自由度的比值。"F"值是均方之比。"p"是经过统计计算得出的每个项的显著性水平。
对于因素A1,我们发现A1对SAS总分有显著的影响(p < 0.05)。具体来说,A1的三个水平之间存在显著的平均差异。在事后多重比较中,我们分别比较了A1中不同水平之间的平均值差异。结果显示,A1的水平1与水平3之间以及水平1与水平4之间的平均值差异是显著的(p < 0.05)。这意味着在A1因素下,不同水平之间存在显著的差异,即A1的水平对SAS总分有影响。
对于因素A2,我们发现A2对SAS总分没有显著的影响(p > 0.05)。具体来说,A2的三个水平之间的平均差异不显著。这意味着在A2因素下,不同水平之间的差异对SAS总分没有明显的影响。
交互作用A1:A2的结果显示,A1和A2之间的交互作用对SAS总分的影响没有显著性(p > 0.05)。这意味着A1和A2的联合作用并没有对SAS总分产生明显的影响。
综上所述,根据双因素方差分析的结果,我们可以得出结论:A1因素对SAS总分有显著影响,而A2因素及A1和A2之间的交互作用对SAS总分没有显著影响。
关注微信公众号发送【示例数据】获取SPSSMAX练习示例数据。
