方差齐性检验用于检验不同样本或组之间的方差是否相等。它是统计分析中常用的一种检验方法，用于判断是否可以应用方差齐性假设。方差齐性检验用于检查两个或多个样本或群体之间的方差是否相等。方差齐性是线性回归、方差分析等许多统计方法的前提假设之一。常用的方差齐性检验方法包括Levene检验和Bartlett检验。如果方差不齐，可能会导致对数据的错误解释和错误推断。

    方差齐性检验用于检查不同样本或群组的数据方差是否相等。当进行一些统计分析，比如方差分析（ANOVA），时，方差齐性是一个重要的假设。如果不满足方差齐性假设，可能需要使用其他的统计方法来分析数据。

    数据说明：

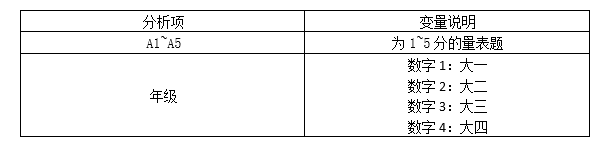
    背景说明：

    这些数据提供了不同年级的F值和p值，用于检验不同年级的数据方差是否相等。可能存在某个变量（比如成绩）在不同年级之间的差异。根据给定的p值，我们可以推测这些年级之间的数据方差在统计意义上没有显著差异。这意味着这些年级之间的数据方差相似，满足方差齐性假设，可以继续使用方差分析等统计方法来分析数据。

    结果显示：

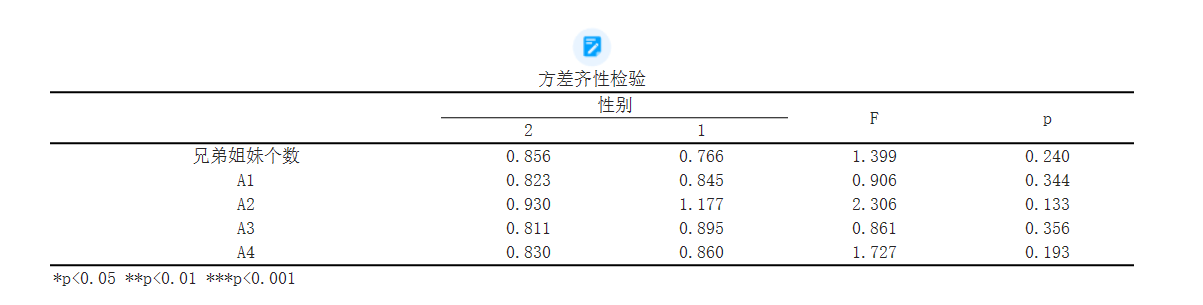
    方差齐性检验的结果显示，对于A1，其F值为0.835，显著性P值为0.479>0.05，水平上不呈现显著性，不能拒绝原假设，因此数据满足方差齐性,可以使用方差分析。

    方差齐性检验的结果显示，对于A2，其F值为1.617，显著性P值为0.192>0.05，水平上不呈现显著性，不能拒绝原假设，因此数据满足方差齐性,可以使用方差分析。

    方差齐性检验的结果显示，对于A3，其F值为1.945，显著性P值为0.129>0.05，水平上不呈现显著性，不能拒绝原假设，因此数据满足方差齐性,可以使用方差分析。

    方差齐性检验的结果显示，对于A4，其F值为0.482，显著性P值为0.696>0.05，水平上不呈现显著性，不能拒绝原假设，因此数据满足方差齐性,可以使用方差分析。

    方差齐性检验的结果显示，对于A5，其F值为2.298，显著性P值为0.084>0.05，水平上不呈现显著性，不能拒绝原假设，因此数据满足方差齐性,可以使用方差分析。

关注微信公众号发送【示例数据】获取SPSSMAX练习示例数据。