spearman相关系数是衡量两个变量的依赖性的非参数指标，被定义成等级变量之间的皮尔逊相关系数。 它利用单调方程评价两个统计变量的相关性。 如果数据中没有重复值，并且当两个变量完全单调相关时，斯皮尔曼相关系数则为+1或−1。

    背景说明：

    所提供的数据是一组变量之间的Spearman相关系数分析结果。Spearman相关系数是一种用于衡量两个等级变量之间相关关系的统计指标，取值范围从-1到1。-1到1。

    相关系数的正负表示变量之间正相关或负相关，而绝对值的大小表示相关程度的强弱。

    在该分析结果中，相关系数后面的星号表示相关性的显著性水平，即*p<0.05表示在显著性水平为0.05下相关性是显著的，**p<0.01表示0.01下相关性是显著的，***p<0.001表示相关性在0.001的显著性水平下是显著的。

    分析结果如下所示：

    由spearman相关性分析可知，

    A1与A2之间的相关性分析结果不显著，不存在显著相关性关系(r=-0.003，p=0.981>0.05)。 A1与A3之间的相关性分析结果显著，成显著正相关关系(r=0.567，p=0.000<0.05)。 A1与A4之间的相关性分析结果显著，成显著正相关关系(r=0.414，p=0.000<0.05)。 A1与A5之间的相关性分析结果显著，成显著正相关关系(r=0.319，p=0.004<0.05)。 A2与A3之间的相关性分析结果不显著，不存在显著相关性关系(r=0.194，p=0.083>0.05)。 A2与A4之间的相关性分析结果不显著，不存在显著相关性关系(r=0.126，p=0.263>0.05)。 A2与A5之间的相关性分析结果不显著，不存在显著相关性关系(r=-0.014，p=0.904>0.05)。 A3与A4之间的相关性分析结果显著，成显著正相关关系(r=0.517，p=0.000<0.05)。 A3与A5之间的相关性分析结果显著，成显著正相关关系(r=0.404，p=0.000<0.05)。 A4与A5之间的相关性分析结果显著，成显著正相关关系(r=0.254，p=0.022<0.05)。

    同时SPSSMAX还提供另一个格式的相关性分析表格。

    相关性分析的热力图输出：

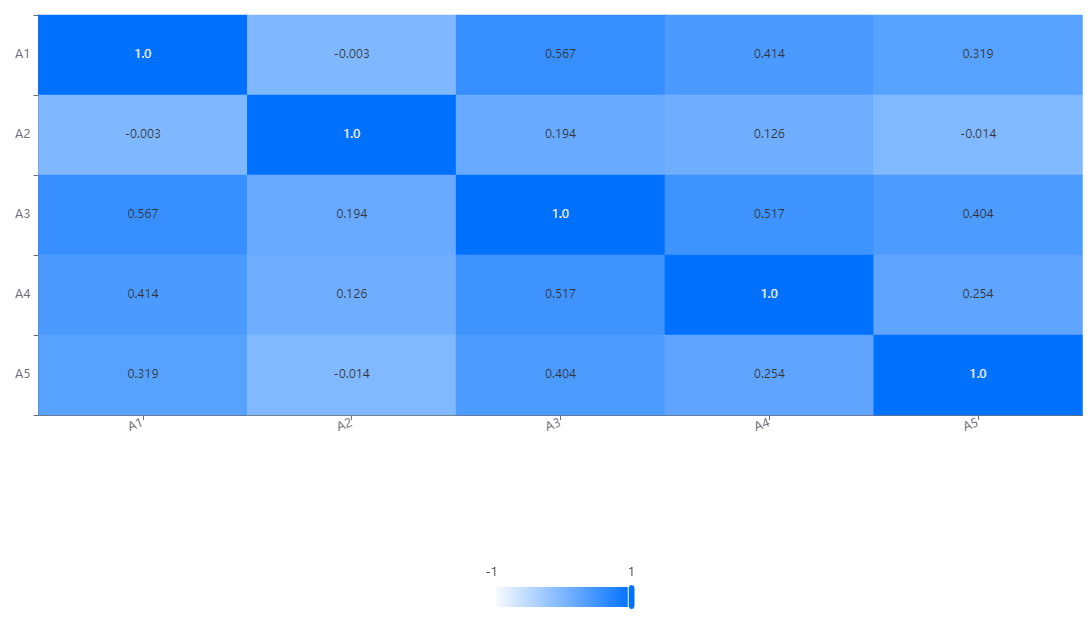
    在相关性热力图中，每个变量都表示为图表中的一个行和列。通过对角线上的单元格，我们可以看到每个变量与自身的相关性，这总是为1，因为一个变量与自身完全相关。

    非对角线上的单元格反映了不同变量之间的相关性。颜色的深浅表示相关性的强度，通常使用颜色渐变来表示。通常，较深的颜色（如深蓝色）表示较强的正相关性，而较浅的颜色（如浅蓝色）表示较强的负相关性。中间的颜色（如白色或浅黄色）表示相关性较弱或接近于零。

    参考文献：

    [1] Fieller, E.C.; Hartley, H.O.; Pearson, E.S. (1957) Tests for rank correlation coefficients. I. Biometrika 44, pp. 470–481

    [2]Piantadosi, J.; Howlett, P.; Boland, J. (2007) 'Matching the grade correlation coefficient using a copula with maximum disorder', Journal of Industrial and Management Optimization, 3 (2), 305–312

    [3]Maritz. J.S. (1981) Distribution-Free Statistical Methods, Chapman & Hall. ISBN 0-412-15940-6. (page 217)

    [4]Myers, Jerome L.; Well, Arnold D., Research Design and Statistical Analysis 2nd, Lawrence Erlbaum: 508, 2003, ISBN 0-8058-4037-0

关注微信公众号发送【示例数据】获取SPSSMAX练习示例数据。